and so the eigenvalues of M are the roots 1, 1 2, 1 + 2 of this polynomial. This leads us to a characteristic polynomial, defined by. Wolfram Knowledgebase Curated computable knowledge powering Wolfram|Alpha. This equation can hold for a nonzero vector v (our eigenvector) only when the determinant of I M is zero. Wolfram Universal Deployment System Instant deployment across cloud, desktop, mobile, and more.
Construct a transition matrix, a Markov Chain, and a Google Matrix for a given web, and compute the PageRank of the web.Wolfram Data Framework Semantic framework for real-world data. 
Apply matrix powers and theorems to characterize the long-term behavior of a Markov chain. Apply theorems to characterize matrices with complex eigenvalues. Use eigenvalues to determine identify the rotation and dilation of a linear transform. Factorize 2 × 2 matrices that have complex eigenvalues. Apply theorems related to eigenvalues (for example, to characterize the invertibility of a matrix). Here is a diagonal matrix and so its eigenvalues are simply the elements on the diagonal. Im need to show that there are no other eigenvalues beside 1 and 0. 
Characterize the invertibility of a matrix using determinants and eigenvalues The curvature of a quadratic form is controlled by the eigenvalues of the matrix. Verify that a scalar is an eigenvalue of a matrix. We will work with a 100x100 symmetric sparse matrix, and make it diagonally.Eigenvalues of a large matrix - Mathematica Stack. Verify that a given vector is an eigenvector of a matrix Here is an example of what I had suggested in a comment. To check the internal stability of the system, calculate the eigenvalues and of the A matrix. For a more advanced tutorial, walk through the. For a 3 by 3 matrix, we need a 3rd fact which is a bit more complicated, and we won’t be using it. Beginners Mathematica Tutorial Introduction This document is designed to act as a tutorial for an individual who has had no prior experience with Mathematica. In fact, it is always true that 1 2 n detA: For a 2 by 2 matrix, these two pieces of information are enough to compute the eigenvalues. Model and solve real-world problems using Markov chains The product of the eigenvalues 1 2 7 3 21 is equal to detA 25 4 21. Compute the area of regions in R^3 under a given linear transformation using determinants. 
Compute determinants of using cofactor expansions and properties of determinants. Upon completion of this course, learners will be able to: Prospective students enrolling in this class are encouraged to first complete the linear equations and matrix algebra courses before starting this class. However, the basic concepts- eigenvectors and eigenvalues-are useful throughout industry, science, engineering and mathematics. The main applications described here are to discrete dynamical systems, including Markov chains. The goal of this part of the course is to decompose the action of a linear transformation that may be visualized. This course then moves on to eigenvalues and eigenvectors.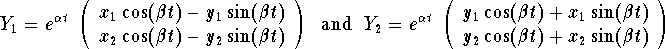 
This idea plays a critical role in computer graphics and in other more advanced courses, such as multivariable calculus. UNIVERSAL BOUNDS FOR EIGENVALUES OF SCHRDINGER OPERATOR ON RIEMANNIAN MANIFOLDS. You will also use the determinant to measure the amount by which a linear transformation changes the area of a region. Annales Academi Scientiarum Fennic Mathematica Volumen 33, 2008, 319-336. The determination of the eigenvalues and eigenvectors of a system is extremely important in physics and engineering, where it is equivalent to matrix diagonalization and arises in such common applications as stability. First, you will be able to apply an invertibility criterion for a square matrix that plays a pivotal role in, for example, the understanding of eigenvalues. Eigenvalues are a special set of scalars associated with a linear system of equations (i.e., a matrix equation ) that are sometimes also known as characteristic roots, characteristic values (Hoffman and Kunze 1971), proper values, or latent roots (Marcus and Minc 1988, p. At the beginning of this course we introduce the determinant, which yields two important concepts that you will use in this course.
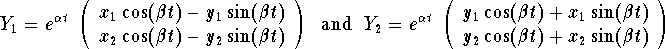
0 kommentar(er)
